Properties of Eigen Values and Vectors

import numpy as np
import seaborn as sns

• A symmetric matrix has real eigen values

# create a symmetric matrix
def get_random_symmetrix_matrix(n=3):
    a = np.random.randint(-10,10, (3,3))
    return (a + a.transpose())/2

s = get_random_symmetrix_matrix()
s

array([[-5. , -2.5, -2. ],
       [-2.5, -9. ,  4.5],
       [-2. ,  4.5,  3. ]])

w, v = np.linalg.eig(s)
w, v

(array([  5.22047873,  -5.17812095, -11.04235778]),
 array([[-0.2587962 ,  0.91904091, -0.29730177],
        [ 0.33248317, -0.20422367, -0.92073212],
        [ 0.90690654,  0.3371298 ,  0.25271333]]))

# check the magnitude of the first eigen vector. 
print(np.dot(v[0], v[0]))

# check the dot product. 
print(np.dot(v[0], v[1]))

# as dimension is one and dot product is close to zero, they are orthonormal

1.0
-1.520268617663237e-16

Power method to find the dominant eigan value

We initialize a random vector x, usually 1s. We multiply ax and divide the output to make the

error = 0.001
n = 3

s = get_random_symmetrix_matrix(n)
x = np.array([1.0] * n)

def get_dominant_eig_value(a):
    eigs = []
    eig_old = None
    x = np.array([1.0] * a.shape[1])
    while True:
        x = np.matmul(a,x)
        eig = np.max(np.abs(x))
        x = x/eig
        if eig_old and abs(eig - eig_old) < error:
            break
        eig_old = eig
        eigs.append(eig)
    return (eig, eigs)
  
dom_eig, eigs = get_dominant_eig_value(s)
print(f'dominant eig is {dom_eig} in {len(eigs)} iterations with margin {error}')

sns.scatterplot(x=range(len(eigs)), y=eigs)

dominant eig is 11.085887005510221 in 6 iterations with margin 0.001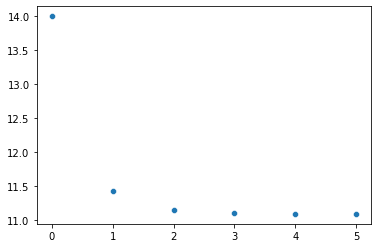

np.abs(

  Input In [6]
    np.abs(
           ^
SyntaxError: unexpected EOF while parsing